

In the seventeenth century two rival theories of the
nature of light were proposed, the wave theory and the corpuscular theory.
The
Dutch astronomer Huygens (1629-1695) proposed a wave theory of light. He believed that
light was a longitudinal wave, and that this wave was propagated through a material called
the 'aether'. Since light can pass through a vacuum and travels very fast Huygens had to
propose some rather strange properties for the aether: for example; it must fill all space and
be weightless and invisible. For this reason scientists were sceptical of his theory.
In
1690 Newton proposed the corpuscular theory of light. He believed that light was shot out
from a source in small particles, and this view was accepted for over a hundred years.
The quantum theory put forward by Max Planck in 1900 combined the wave theory
and the particle theory, and showed that light can sometimes behave like a particle and
sometimes like a wave. You can find a much fuller consideration of this in the section on the
quantum theory.
As we have seen,
Huygens considered that light was propagated in longitudinal waves through a material
called the aether. We will now look at his ideas more closely.
Huygens published his
theory in 1690, having compared the behaviour of light not with that of water waves but with
that of sound. Sound cannot travel through a vacuum but light does, and so Huygens
proposed that the aether must fill all space, be transparent and of zero inertia. Clearly a very
strange material!
Even at the beginning of the twentieth century, however,
scientists were convinced of the existence of the aether. One book states 'whatever we
consider the aether to be there can be no doubt of its existence'.
We now consider
how Huygens thought the waves moved from place to place.
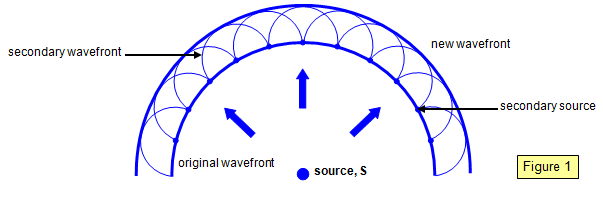
Consider a wavefront
initially at position W, and assume that every point on that wavefront acts as a source of
secondary wavelets. (Figure 1 shows some of these secondary sources). The new wavefront
W1 is formed by the envelope of these secondary wavelets since they will all have moved
forward the same distance in a time t (Figure 1).
There are however at least two problems with this
idea and these led Newton and others to reject it:
(a) the secondary waves are
propagated in the forward direction only, and
(b) they are assumed to destroy each other
except where they form the new wavefront.
Newton wrote: 'If light consists of
undulations in an elastic medium it should diverge in every direction from each new centre of
disturbance, and so, like sound, bend round all obstacles and obliterate all shadow.' Newton
did not know that in fact light does do this, but the effects are exceedingly small due to the
very short wavelength of light.
Huygens' theory also failed to explain the rectilinear
propagation of light.
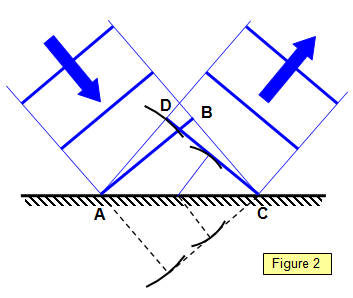
The reflection of a plane wavefront by a plane mirror is shown
in Figure 2. Notice the initial position of the wavefront (AB), the secondary wavelets and the
final position of the wavefront (CD). Notice that he shape of the wavefront is not affected by reflection at a
plane surface.
The lines below the mirror show the position that the wavefront would
have reached if the mirror had not been
there.
We will now show how Huygens'
wave theory can be used to explain reflection and refraction and the laws governing
them.
Consider a parallel beam of monochromatic light incident on a plane surface, as shown in Figure 3. The wave fronts will be plane both before and after reflection, since a plane surface does not alter the shape of waves falling on it.
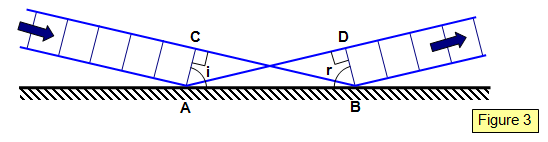
Consider a point where the
wavefront AC has just touched the mirror at edge A. While the light travels from A to D, that
from C travels to B. The new envelope for the wavefront AC will be BD after reflection.
Therefore: AD = CB, Angle ACB = angle ADB = 90o, AB is
common
Therefore ΔACB and ΔBDA are similar and so angle CAB = angle BAD.
Therefore i = r and the law of reflection is proved.
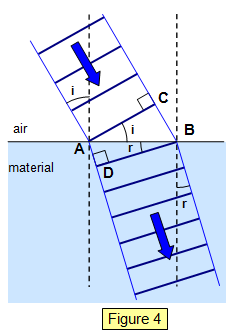
Consider a plane monochromatic wave hitting the surface of
a transparent material of refractive index n. The velocity of light in the material is cm and that
in air ca. Now in Figure 4,
CB = AB sin i
AD = AB sin r
The same
argument applies about the new envelope as in the case of reflection:
time to travel
CB = CB/ca = AB sin i/ca
time to travel AD = AD/cm = AB sin i/cm
But these are equal
and therefore:
ca/cm = sin i/sin r = anm.
This is Snell's law, and it was verified
later by Foucault and others.
Notice that since the refractive index of a transparent
material is greater than 1, Huygens' theory requires that the velocity of light in air should be
greater than that in the material.
Newton proposed that light is shot out from a source as a stream of
particles. He argued that light could not be a wave because although we can hear sound
from behind an obstacle we cannot see light - that is, light shows no diffraction. He stated
that particles of different colours should be of different sizes, the red particles being larger
than the blue.
Since these particles are shot out all the time, according to Newton's
theory, the mass of the source of light must get less!
We can use Newton's theory
to deduce the laws of reflection and refraction.
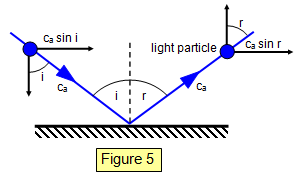
Consider a particle of light in collision with a mirror. The collision is supposed to be perfectly elastic, and so tile component of velocity perpendicular to the mirror is reversed while that parallel to the mirror remains unaltered.
Newton
assumed that there is an attraction between the molecules of a solid and the particles of
light, and that this attraction acts only perpendicularly to the surface and only at very short
distances from the surface. (He explained total internal reflection by saying that the
perpendicular component of velocity was too small to overcome the molecular attraction.)
This has the effect of increasing the velocity of the light in the material.
Let the velocity
of light in air be ca and the velocity of light in the material in Figure 6 be cm.
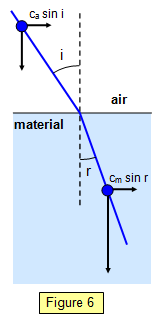
The velocity parallel to the material is unaltered
and therefore:
casin i = cmsin r
Therefore:
cm/ca = sini/ sinr =
anm
This ratio is the refractive index, but because n > 1 the velocity of light in the
material must be greater than that in air. Newton accepted this result and other scientists
preferred it to that of Huygens, mainly because of Newton's eminence.
A problem of
the corpuscular theory was that temperature has no effect on the velocity of light, although
on the basis of this theory we would expect the particles to be shot out at greater velocities
as the temperature rises.
| Wave theory | Corpuscular theory | |
| Reflection | Reflection | |
| Refraction | Photoelectric effect | |
| Diffraction | ||
| Interference |